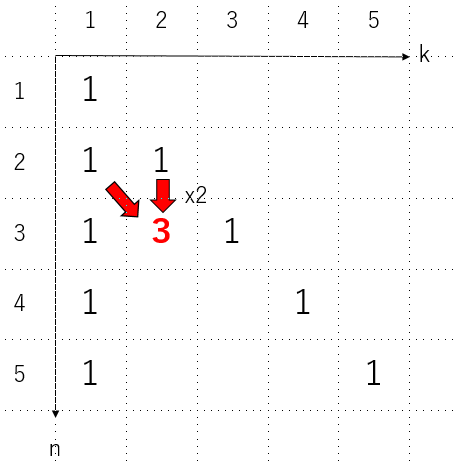
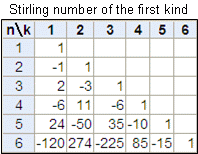
写像12相をいちから勉強してatcoderの組合せ 数え上げ問題をクリアしたいと思ったけどまだまだ知らない事が多いと強烈に感じた Ctoを目指す日記
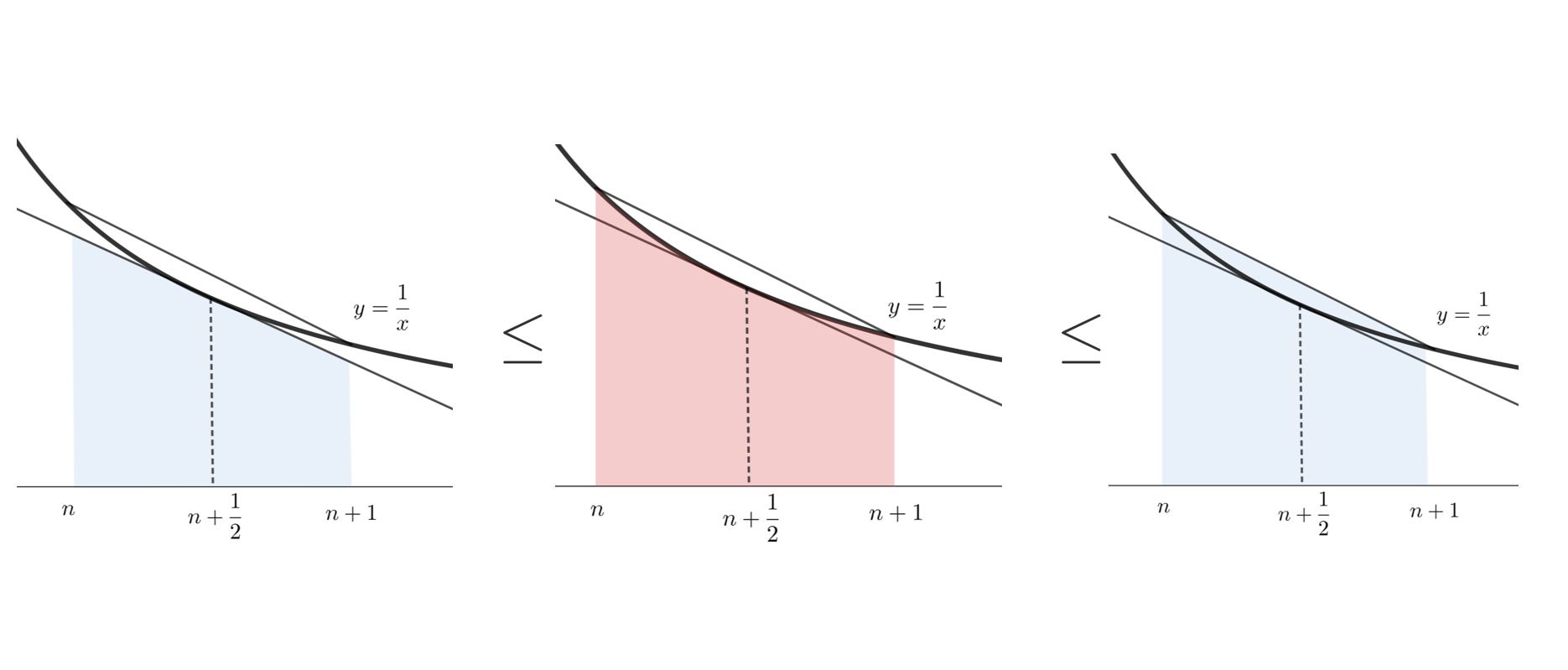
解説 『極秘空輸』アップデートで追加された航空機。 モデルは第二次世界大戦中にドイツが開発した世界初のロケット戦闘機「メッサーシュミットMe163コメート」。 ジェット推進ではなくロケット推進となっている機体である。 先端のプロペラは速風を スターリングの公式 自然数 N N が十分に大きい場合に、 N N の階乗の対数は と近似できる。 この近似を スターリングの公式 (Stirling's formula) という。 証明 次の積分 (1) (1) に着目し、積分区間を幅が 1 2 1 2 の区間に分けて と表す。 さらに右辺を奇数項と偶数項に分けてまとめると、 (2) (2) と表せる。 ここで被積分関数 logx log x は単調増加関数 であるので、 区間 (n,n 1 2 ( n, n
スターリング 数学
スターリング 数学-スターリンク (Starlink )は、アメリカ合衆国の民間企業スペースX社が運用している衛星コンステレーション 。 低コスト・高性能な衛星バスと地上の送受信機により、衛星インターネットアクセスサービスを提供することを目的とする 。 年、北アメリカ大陸とヨーロッパで試験運用が始まっ POINT スターリングの公式の異なる2つの表式の関係. 統計力学でよく出てくるStirlingの公式について考察します. スターリングの公式の2つの表式 式 (1)の導出 2式の関係について 付録 計算メモ スターリングの公式の2つの表式スターリングの公式(Stirling's approximation/Stirl
2項係数 スターリング数 分割数
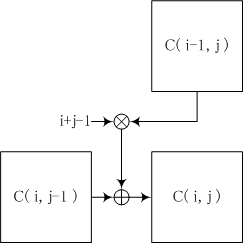
個のグループに分けるやり方の総数を第2 種のスターリング 数といい, S(n,r) で表す. 異なる 個のものから 個取り出す取り出し方の総数は, nCr とかくので,これにならっ て,以後 S(n,r) n S r と表すことにしよう.ここで, nSn1 nS00 である. 例 5人を2組に分けるやりかたの総数は何通りか ① 1 人4 人の場合 5 C 1 u 4C 45 通り ② 2 人3 人の場合 5 C2 u 3C 310 通り ①②より 5S25 10 15 通り 例 6スターリングの公式はガンマ関数の漸近展開から導出される。 この節ではガンマ関数の基本的な性質について復習するが、すでによく知っている人は次の節まで読み飛ばしてよい。 α > 0 とするとき、ガンマ関数は次の積分で定義される: (1) (1) Γ ( α) = ∫スターリングの公式による階乗・順列・組み合わせの近似計算 スターリングの公式で近似計算します。指数部を分けて計算・表示するので、大きい値でもオーバーフローしません。 値を入力してエンターを押してください。 階乗 n!!
スターリング エンジンの しかし、当時は高圧(大気圧以上・・・当時は数気圧~10気圧)に耐えうる蒸気缶を製造する鋳造技術が未熟で、鋳物に、 いわゆる"巣(空気泡)"ができ、そのために、高圧に耐えられず蒸気缶が爆発する事故が度々発生し この S ( n, k) を 第二種スターリング数 (Stirling number of the second kind) と呼びます。 すぐわかる S ( n, k) の性質として、 n = k の時には、要素を一つずつばらすしかないので一通り、つまり S ( n, n) = 1 です。 また、グループが一つしかない場合にも、分け方は一通りしかないので S ( n, 1) = 1 が成り立ちます。 要素を一つも含まないグループを作ってはいけないという制約から、グ t分布は、サンプル数が増えると標準正規分布に近づく t分布と標準正規分布の関係は、スターリングの公式を使って証明できる 参考文献 こんにちは、みっちゃんです。 今回の記事では、正規分布にしたがう母集団に関する分布について有名な「t分布
スターリング 数学のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「スターリング 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「スターリング 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「スターリング 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
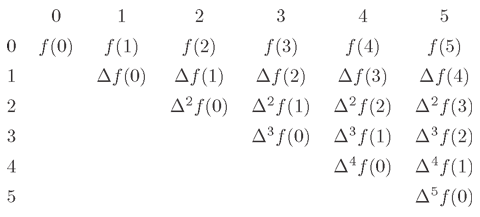 |  |  |
 |  |  |
「スターリング 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | 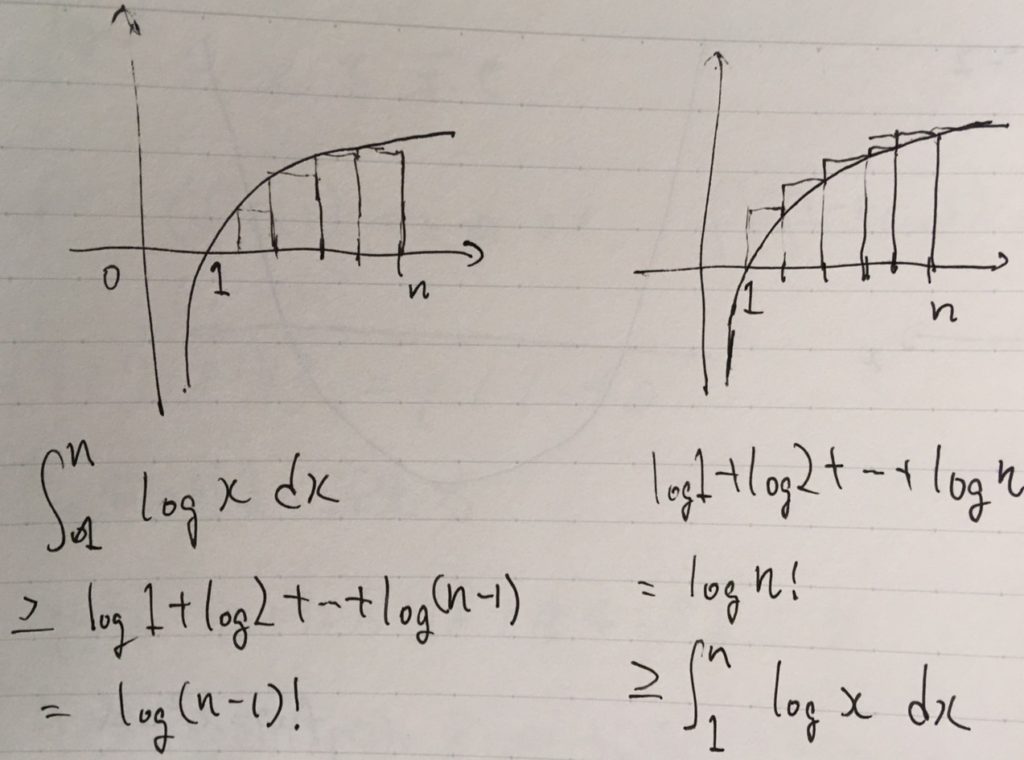 | |
「スターリング 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 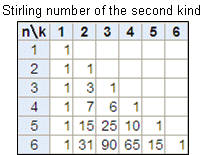 |  |
 | ||
 |  |  |
「スターリング 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  | |
「スターリング 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 | ||
「スターリング 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
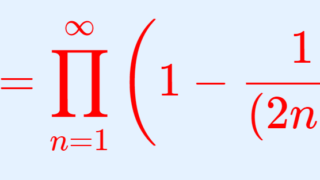 |  |  |
 |  |  |
 | ||
「スターリング 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「スターリング 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「スターリング 数学」の画像ギャラリー、詳細は各画像をクリックしてください。
 |
関Bernoulli数は第二種Stirling数を用いて表すことができます。関Bernoulli数については関ベルヌーイ数 INTEGERSを、第二種Stirling数についてはBell数の母関数表示と第二種Stirling数 INTEGERSを参照してください。関Bernoulli数は一つ目の記事で紹介したようにを満たすように定義されます。一方、二つ目を指数関数で近似する公式です。 統計力学(物理の一分野)や組み合わせ数学で用いられます。 階乗よりも指数関数の方が扱いやすい場合が多い ので嬉しいです。 スターリングの公式の別バージョン スターリングの公式には n!\fallingdotseq\sqrt {2\pi n}\left (\dfrac {n} {e}\right)^n n!
Incoming Term: スターリング 数学, スターリング 数学者,




0 件のコメント:
コメントを投稿